Šifry a šifrování

Zajímají vás principy šifer, rozdílu mezi symetrickými a asymetrickými algoritmy a kryptografie vůbec? Tento článek vás zavede to temného světa šifrování.

Základní princip šifrování je následující:

• Vezmeme zprávu (tzv. otevřený text) a aplikujeme na ni šifrovací algoritmus.
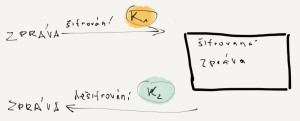
• Šifrovací algoritmus je přesně definovaný postup kroků, který se používá k převodu z každému dobře srozumitelného obsahu do zašifrované podoby. K tomu, aby výstup byl unikátní, se pak používá šifrovacího klíče K1.
• Zašifrovaný obsah se distribuuje k příjemci (adresátovi zprávy). Je potřeba počítat s tím, že na trase může dojít k odposlechu.
• Příjemce k tomu, aby zprávu mohl rozlousknout, použije dešifrovacího algoritmu (jedná se zpravidla inverzního postup k šifrování) a dešifrovacího klíče K2. Šifrovací a dešifrovací klíče K1 a K2 mohou, ovšem nemusí být totožné.

Problém digitalizace

Předtím, než můžeme začít s účinným převodem obsahu na šifru, je však potřeba převést ho na digitalizovaný vstup. Jak známo, naše smysly přijímají analogové signály, zatímco matematické funkce a počítače dovedou zpracovávat pouze digitalizované hodnoty. Proto je potřeba provést vždy předtím, než začneme šifrovat, převod do digitální soustavy.

Převod je vždy spojen se ztrátou informace. Na druhou stranu, zatímco analogový signál může mít (a ve většině případů má) ztráty při přenosu, signál digitální se již dá přenášet, jednoduše duplikovat a dále zpracovávat bez dalších následných ztrát. Převod z analogového do digitálního signálu se zpravidla skládá z následujících posloupností:

Symetrické šifry

Jedná se o tradiční typ šifer. Jejich šifrovací algoritmus je založen na tom, že je potřeba utajit jak šifrovací, tak dešifrovací klíč – jednoduše z toho důvodu, že se jedná o ten samý klíč, liší se pouze algoritmy, do kterých se dosazuje. Z toho plyne, že při použití tohoto typu šifer je potřeba bezpodmínečně zatajit šifrovací klíč (tj. na našem obrázku K1, který je totožný s K2).

Klasickými kryptoalgoritmy, které vycházejí z tohoto principu jsou například substituční šifry, kde se vždy nahrazuje určité písmeno posunem o jiné. Z nich jsou neznámější následující:

Césarova šifra

Jednoduchá kryptografická metoda založená na tom principu, že se posune písmeno o x znaků v latinské abecedě a adresát s odesílatelem se dohodnou na hodnotě posunu x. Např.: dohodneme se na hesle 4 (tj. posunu o 4 znaky) a kódujeme:

a  > e

h > l

o > s

j > n

takže z otevřeného textu „ahoj“ vznikne zašifrovaná zpráva „elsn“. Převod nemusíte provádět ručně, využít můžete pro tuto šifru například tento online nástroj.

Vigenérova šifra

Relativně pokročilý způsob šifrování, oblíbený zejména v 19. století. Základem je tzv. Vigenérův čtverec.

Princip kódování je s pomocí čtverce už relativně jednoduchý: určíme klíč v podobě slova (např. ahoj) a šifrujeme text tak, že cyklicky nahrazujeme písmena za jiné podle použitého klíče. Do řádku se dosazuje otevřený text, do sloupce pak klíč, tam kde se písmena spojí pak vychází šifrovaný text. Nástroj pro kódování pomocí Vigenérovy tabulky online najdete například zde.

Vernamova šifra

Jako jediná ze subsitutčních šifer odolává odhalení z toho důvodu, že se při šifrování používá stejně dlouhý klíč, jako je samotná zpráva a v ideálním případě tak existuje nekonečné množství kombinací, které mohou vzniknout, tím pádem ani útok „hrubou silou“ nemůže šifru odhalit. Zpravidla se kódování provádí tak, že se zadá například číslo strany v určité knize, jejíž text se použije jako klíč a následně se šifruje skrze Vigenérův čtverec – tento princip šifrování je popsán ve Švejkovi, kdy ho používala Rakousko-Uherská armáda při komunikaci na frontě. Mechanickým zařízením, blížícím se dokonalostí a „neprůstřelností“ této šifře byl německý kódovací stroj Enigma, ve kterém se používaly ke kódování kotouče obsahující permutace latinské abecedy a kód se zadával pomocí jejich unikátního sestavení.

Nevýhodou substituční kryptografie je to, že většina zašifrovaných kódů se dá poměrně dobře krypotanalýzou rozbít. Používá se k tomu například následujícího:

• Pro jednotlivé jazyky je známo, jak se průměrně často vyskytují jednotlivá písmena. Z toho plyne, i když v celém textu nahradíme písmeno A písmenem Z, které se pak místo něj ocitne v zašifrovaném textu, nijak nám to nepomůže, protože útočník jednoduše zjistí, že písmeno Z se vyskytuje obdobně často v šifrovaném textu, jako písmeno A v běžném textu a z toho pak může na základě dalších znaků odhalit klíč.
• Obdobně je známa míra koincidence – tj. pravděpodobnost výskytu totožného znaku dvakrát vedle sebe.
• Dalším prvkem, který se analyzuje, je výskyt totožných skupinek písmen v textu vedle sebe – z toho, jak jsou daleko od sebe, se dá odhadnout posun textu.

Asymetrické šifry

Asymetrické šifrování je novinkou, která se začala používat až ve 20. století. Při použití tohoto šifrovacího postupu není šifrovací klíč K1 a K2 totožný, ale liší se. Při kódování je použit klíč K1 a při dešifrování klíč K2. Když příjemce zná šifrovací algoritmus i šifrovací klíč, stále nemá vyhráno, protože to, co potřebuje ke správné interpretaci šifry, je dešifrovací klíč K2. Při konstrukci těchto kryptoalgoritmů zpravidla dochází k rozkladu kódovacích klíčů a jejich základem je neřešitelná nebo obtížně řešitelná matematická úloha.

Byly vyvinuty a pro různé účely se dosud využívají:

Kódování založené na problému batohu

Problém batohu je optimalizační úloha, založená na rozdělení určitého počtu předmětů na omezený prostor. Obtížná řešitelnost této úlohy je základem kódovacího algoritmu, který se ale podařilo nedávno prolomit.

Šifra RSA

Je založena na následujícím postupu šifrování a dešifrování:

c = m^e mod n

m = c^d mod n

kde m je původní zpráva, c šifra a, e veřejný šifrovací exponent, d soukromý dešifrovací exponent a n tzv. veřejný modul. Tento algoritmus je dosud při dostatečné délce klíče považován za bezpečný.